Students begin learning about shapes in Kindergarten. They learn how to notice their differences in size, color and shape. They assign names to figures and learn that things can be called squares or triangles.
As students extend their mathematical understanding, they learn that these shapes can have different names based on their attributes. Triangles can be named by the length of their sides or the types of angles they have. They could even be called two different names depending on what one is describing.
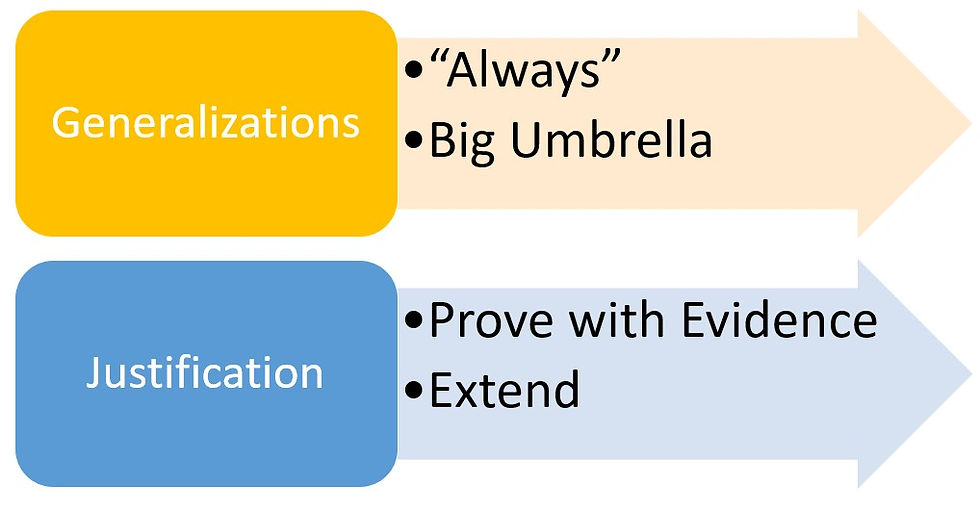
This is the process of moving from basic generalizations to justification. In lower grades, we tell students, "this is a rectangle" and "this is a square". Then, students learn in Grade 3 or Grade 4 that a square is always a rectangle but a rectangle is sometimes a square. Students must justify their thinking by measuring the length of the sides. They move from big umbrella generalizations to justifications that describe their thinking and narrow it down.
As math educators, we have to be careful not to let students get stuck in these "big umbrella" ideas. We have to challenge them with tough questions and help them to realize that there are some always rules, but there are also some situations that depend on a set of variables.
For example, telling students that they should always start in the ones place when subtracting. This is a broad generalization. A student doesn't have to start in the ones place. It can be easier when regrouping, but it is not completely necessary. And what happens when they start learning about decimals? Where does a student start then? A broader generalization might be that is can be easier to start in the place of least value when regrouping is involved.
Encouraging students to think about concepts in this way will help them become rich thinkers. Concept mapping and higher order thinking skills will help to accomplish this. One of my favorite activities is to compare and contract with shapes. By using a simple venn diagram, students can begin having these types of conversations where they explore when a shape might be called one thing or even called another.
The goal is to help our students leave behind rigid thinking and become fluid problem solvers. Students can learn that sometimes they may label a figure as a quadrilateral with 4 sides but it may be a rhombus if those sides are equal and there are no right angles. Learning these specific parameters will help them narrow down their understanding and prove their thinking.
This tends to be a Grade 5 expectation, because at this age, students should have more background knowledge that they can use to be flexible thinkers. Check out this freebie below where students can use these graphic organizers to compare figures. Provide students with regular pattern blocks at first and ask them to place them where they belong. As students become more proficient, provide pictures of other shapes that have different length sides and angles to extend their thinking. Encourage students to use the following prompts:
________ is a ________ but also a __________. Example: A rhombus is a parallelogram but also a quadrilateral.
________ is a ________ but never a __________. Example: A rhombus is a quadrilateral but never a square.
Remind students that they can make several different statements based on what they know about the sides and angles of each figure. Download three different graphic organizers for free by entering in your email below.
To apply these strategies, check out this free resource Finding Surface Area of Solids Using Plane Shapes.
You can also check out my Flat and Solid Shapes Bundle in the SHOP. Members, don't forget to use your discount!
コメント