Students begin learning about plane shapes in Kindergarten for a reason. Their understanding of plane shapes helps them with later concepts with solid figures. Think about it: They begin learning about the number of sides and angles for each plane shape. They learn how these plane shapes form solid shapes. Solid shapes can roll, stack or slide based on their properties.
As students move into fifth and sixth grade, they use this foundation to learn about surface area and volume. These are practical life skills that matter. Ever tried to determine how much liquid a container can hold or how much paper is needed to wrap gifts? (I look at the dimensions of wrapping paper every holiday season.)
When I was growing up, I had to memorize formulas. I can remember stressing each night before a test trying to remember what needed to be multiplied by what. Often, I would forget...or get them mixed up. Ultimately, I would get it wrong if I didn't remember.
This practice did not show my understanding of these concepts. The memorization of formulas showed whether I had a good memory and the fact that I couldn't reason through what I was solving. And guess what? 20 years later...I still don't remember that formula.
I recently read an article where someone described learning math as learning your way around the park. Someone can tell you exactly how to get to from Point A to Point B by very specific directions. But what happens when you get confused or make a wrong turn? Someone else might let you explore the park and start to notice landmarks and features to help identify places in the park. Then when trying to get from Point A to Point B, you could orient yourself with what's around you. It's OK that you forgot the directions, because you have familiar points along the way to help you get there.
So what if we taught students to use what they already know from Kindergarten to reason through what they are trying to solve. For example, if I'm finding the surface area of a cube, I can think about what I know about the area of a square.
What plane shapes are used to create a cube?
What special attributes are unique to squares?
How can these attributes help me find the area?
How is finding the area like an array?
How does it demonstrate multiplication?
Once I know the area of 1 square, how can I use that area to find the area of 6 squares?
By using what students already know, we are doing two things: We are helping connect long-term memory to new ideas, and we are giving them the confidence to find a solution even if they don't remember a formula.
Check out this easy activity where students use a graphic organizer to outline what they know and combine it to find the surface area. It can be done using nets or solids. Students just need to break apart what they know using plane shapes and combine the areas.
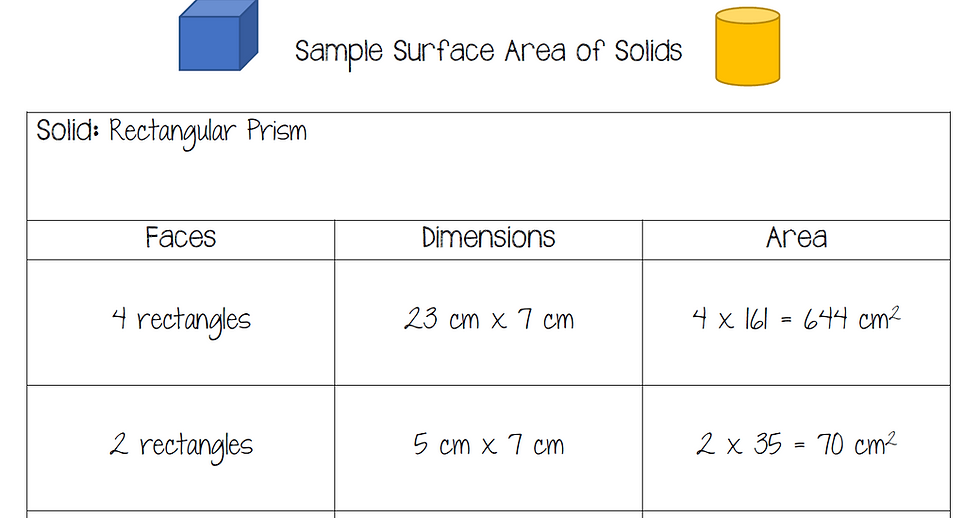
Think about how nice it is to take such a complicated task (multiple operations, multiple steps) and break it down into something manageable. Grab your FREE download of this graphic organizer and some solid cards to watch your students gain confidence working challenging problems! Don't forget to check out the 3 teaching videos that accompany this task in my Teaching and Learning Library. Check out your membership with a 2-week money back guarantee!
Finding Surface Area
Finding Nets of Solids
Finding Surface Area of Cubes
Finding Surface Area of Rectangular Prisms